In
this lesson, you will learn how to create a steering wheel that you can
control its left-right turning by hotkey and it remains in the same
position (using Move command).
You can
simply apply the same template to any props that need rotation control
where the prop remains in the same position. E.g. Things like Tank
Turrets, Radars, windmills, compasses, anemoscopes even vehicles like
tanks can rotate at the same location.
- Select
Move Command from the command drop
down list. Click "Add".
- Move Template floater pops up. Focus in the
Type section, type allows you to set the hot key combinations
for you to use in iClone. This corresponds to the hot keys of the move
command.
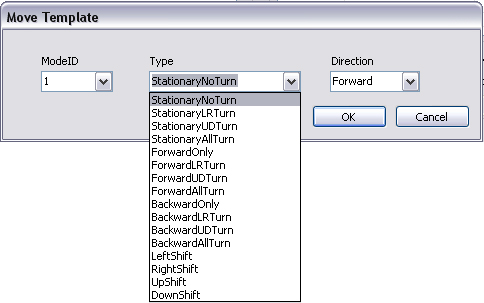
- In this tutorial we will focus on StationaryNoTurn,
StationaryLRTurn, StationaryUDTurn and StationaryAllTurn.
-
StationaryNoTurn, the prop
remains in the same position without turning motions.
- StationaryLRTurn,
the prop remains in the same position with left and right
turning
motions like yaw turning.
- StationaryUDTurn,
the prop remains in the same position with up and down
turning motions like pitch turning.
- StationaryAllTurn,
the prop remains in the same position with all turns.
- Select StationaryLRTurn
and rename the command "Stationary_Rotation".
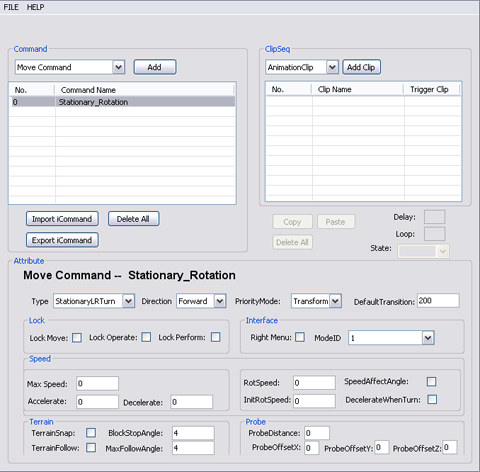
- Set RotSpeed and InitRotSpeed
for the Stationary_Rotation command.
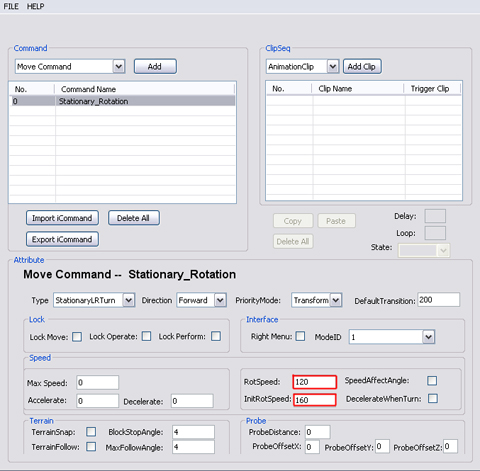
-
RotSpeed
defines the rotation speed you set for the selected item. This
means how quickly your object will turn. Higher the setting, the
faster the turn (but will have a snapping effect, but this will
ensure sharper turns). Lower the setting means smoother curves,
but this means sharp turns could not be made (similar to the
concept of a car turning, a car can never make a 90 degree turn).
-
InitRotSpeed
defines the speed which first must be exceeded before rotation
(turning) can begin. When InitRotspeed is defined as zero, then
when the prop rotates it will have the setting of the speed of
RotSpeed attribute.
- Save the DramaScript and import it into the
prop to test out the speed.
|


